2019 Leetcode

blairchen

Publish：Jul 1, 2019

1、七种常见的数组排序算法整理(C语言版本)
2、2019 算法面试相关(leetcode)–数组和链表
3、2019 算法面试相关(leetcode)–字符串
4、2019 算法面试相关(leetcode)–栈和队列
5、2019 算法面试相关(leetcode)–优先队列
6、2019 算法面试相关(leetcode)–哈希表
7、2019 算法面试相关(leetcode)–树、二叉树、二叉搜索树
8、2019 算法面试相关(leetcode)–递归与分治
9、2019 算法面试相关(leetcode)–贪心算法
10、2019 算法面试相关(leetcode)–动态规划(Dynamic Programming)

Hot100

hot easy

两数之和， ✔️

反转链表，回文链表(1.快慢p拆，2.翻转 3. 判断)，相交链表（f1: set() f2: A+B和B+A f3:快慢p） ✔️

最大子序和（动态规划/分治法）， ✔️

爬楼梯，打家劫舍 & 环形链表 , 合并2个有序链表， ✔️

有效的括号，最小栈 ✔️

买卖股票的最佳时机-3, 两阶段， ✔️

买卖股票的最佳时机-4, 超难

翻转二叉树 , 把二叉搜索树转换为累加树， ✔️

只出现一次的数字，汉明距离 x&(x-1)来统计二进制数x中1的个数 ✔️

二叉树的直径 & 二叉树的最大深度 & 对称二叉树, 合并二叉树， ✔️

求众数，移动零，找到所有数组中消失的数字

最短无序连续子数组,找到字符串中所有字母异位词 , 路径总和 III

hot 中等

Page1

两数之和（方法：一遍哈希表） Map < Integer, Integer > ， ✔️

最长回文子串

反转链表， ✔️

LRU缓存机制

编辑距离

无重复字符的最长子串

戳气球

接雨水

两数相加 (链表+进位carry)， ✔️

寻找两个有序数组的中位数

三数之和（2方法： hash & 对撞指针）， ✔️

最大子序和（动态规划/分治法）， ✔️

字符串解码

删除无效的括号

最大矩形有难度 nok

全排列 (交换法，类比字符串思路)， ✔️

合并两个有序链表， ✔️

正则表达式匹配

零钱兑换， ✔️

Page3

单词搜索 (DFS vector < vector < bool > > visit(row, vector < bool > (col, false)))

打家劫舍之三 (DFS)

最小路径和

电话号码的字母组合

每日温度

回文子串

验证二叉搜索树

单词拆分

颜色分类

在排序数组中查找元素的第一个和最后一个位置

字母异位词分组

完全平方数

环形链表 II

除法求值

课程表

根据身高重建队列

除自身以外数组的乘积

目标和

比特位计数

public class Solution {
    public int[] twoSum(int[] nums, int target) {
        HashMap<Integer, Integer> m = new HashMap<Integer, Integer>();
        int[] res = new int[2];
        for (int i = 0; i < nums.length; ++i) {
            if (m.containsKey(target - nums[i])) {
                res[0] = i;
                res[1] = m.get(target - nums[i]);
                break;
            }
            m.put(nums[i], i);
        }
        return res;
    }
}

爬楼梯

1. Array

1.1 easy

二维数组中的查找 bool Find(int b[][4], int rows, int cols, int value)， ✔️

替换空格 char* replace(char* str, int len) ‘ ’->%20 在源数组总长度，从后向前，逐个赋值， ✔️

数字在排序数组中出现的次数 biSea(arr,k+0.5)-biSea(arr,k-0.5); / bina(*a, len, num, isLeft)， ✔️

旋转数组的最小元素 while(low < high) { if(a[m] > a[high]) min[m+1,high], else [low,m]} ✔️

调整数组位数使奇数位于前面 void odds(int[] arr) ， ✔️

次数超过一半的次数 * int core(int *a, int len)， ✔️

丑数, 只包含质因子2、3和5的数称作丑数, 1, 2, 3, 5, 6, … ， ✔️

和为S的两个数字(双指针思想) ， ✔️

扑克牌顺子 (排序后，统计大小王数量 + 间隔)， ✔️

构建乘积数组 (A数组，从前向后，再从后向前j-2,构造 B)， ✔️

求1+2+3+…+n (判断 && 递归)， ✔️

1.2 medium

八皇后， void dfs(int n) for(int i = 0; i < 8; i++) { pos[n] = i; ， ✔️

和S连续正数序 (3fun，mid = (1+sum)/2; while(start<mid), Sum(int start, int end), 双vector)， ✔️

约瑟夫环 LinkedList; (index = (index + m) %link.size();link.remove(index--)😉 link.get(0); ， ✔️

数组排成最小的数 Arrays.sort(str, new Comparator(){ public int compare(String s1, String s2)，✔️

数组中只出现一次的数字 , 划分2数组，num & (-num);二者与后得到的数，将num最右边的1保留下来，✔️

1.3 important

数组中的逆序对(归并排序). void mergeSort(int a[], int l, int r) ， ✔️

最小的K个数(堆排序)，数据流中的中位数（2 PriorityQueue）.

最小的K个数 （2fun）快排思想 part return l, 外else return left; void set_k(int* input, n, k) ， ✔️

quickSort(a[],left,right), while(1) { (双while, if(l >= r) break; swap) } swap(a[left], a[l]);， ✔️

最短路Floyd， ✔️

quickSort (1 while + [2while + break + swap] + swap + 2 quickSort)

mergeSort (2 mergeSort + new *arr + 3 while + 1 for)

1.1 八皇后

const int N = 105;
int pos[N];
int num = 8, cnt = 0;
bool ok(int n) {
    for(int i = 0; i < n; i++) {
        if(pos[i] == pos[n]) return false;
        if(abs(pos[n] - pos[i]) == n-i) return false;
    }
    return true;
}
void dfs(int n) {
    if(n == num) {
        cnt++;
        return;
    }
    for(int i = 0; i < num; i++) {
        pos[n] = i;
        if(ok(n)) {
            dfs(n+1);
        }
    }
}
int main() {
    res = dfs(0);
    cout << res << endl;
    return 0;
}

1.2 二维数组中的查找

int a[][4] = {
    { 1, 2, 3, 4 },
    { 5, 6, 7, 8 },
    { 9, 10, 11, 12},
    { 13, 14, 15, 16},
    { 17, 18, 19, 20}
};

bool Find(int b[][4], int rows, int cols, int value) {
    
    int row = 0, col = cols - 1;
    
    while (b != NULL && row < rows && col >= 0) {
        
        if (b[row][col] == value) {
            cout << "row: " << row << " col: " << col << end;
            return true;
        }
        else if (b[row][col] > value) {
            col--;
        }
        else {
            row++;
        }
    }
    return false;
}

1.3 替换空格

char* replace(char* str, int len) {    
    while(str[len] != '\0'){
        if(str[len] == ' '){
            konglen++;
        }
        len++;
    }
    return '\0';
}

1.4 旋转数组的最小元素

void quickSort(int a[], int left, int right) {
    if(left < right) { // exit. good idea!
        int l = left, r = right, x = a[l];
        while(1) {
            while(l < r && a[r] >= x) r--;
            while(l < r && a[l] <= x) l++;
            if(l >= r) break;
            swap(a[r], a[l]);
        }
        swap(a[left], a[l]);
        quickSort(a, left, l-1);
        quickSort(a, l+1, right);
    }
}

1.5 调整数组位数使奇数位于前面

void reorderOddEven(int[] arr, len) {
    if (arr == NULL || len <= 1 ) {
        return;
    }
    int l = 0, r = len - 1;
    while (l < r) {
        while (l < r && arr[r] % 2 == 0) {
            r--;
        }
        while (l < r && arr[l] % 2 == 1) {
            l++;
        }
        if (l < r) {
            swap(arr[l], arr[r]);
            l++, r--;
        }
    }
}

1.6 出现次数超过一半的次数

int core(int *a, int len) {
    if (arr == NULL || len <= 0 ) {
        return;
    }
    int target = a[0], cnt = 1;
    
    for (int i = 1; i < len; i++) {
        if (a[i] == target) {
            cnt++;
        }
        else {
            cnt--;
            if (cnt == 0) {
                target = a[i];
                cnt = 1;
            }
        }
    }
    return target;
}

1.7 最小的K个数 part 快排思想

const int N = 105;
int a[N] = {4, 5, 1, 6, 2, 7, 3, 8};
int part (int *a, int left, int right) {
    
    if(left < right) {
    
        int x = a[0], l = left, r = right;
    
        while(l < r) {
            while(l < r && a[r] >= x) r--;
            while(l < r && a[l] <= x) l++;
            if(l >= r) break;
            swap(a[l], a[r]);
        }
    
        swap(x, a[l]);
        return l;
    }
    
    else return left;
}

void set_k(int *input, int n, int k) {
     
    if(input == NULL || k > n || k <= 0 || n <= 0) {
        return;
    }
    int start = 0, end = n - 1;
    
    int index = part(input, start, end);
    
    while(index != k-1) {
        
        if(index > k-1) {
            end = index - 1;
        }
        else if(index < k - 1) {
            start = index + 1;
        }
        else {
            break;
        }
        index = part(input, start, end);
    }
}

1.8 数组中的逆序对 & 归并排序

void mergeSort(int a[], int l, int r) { //  8, 5, 4, 9, 2, 3, 6
    if(l >= r) return;   // exit.
    int mid = (l+r) / 2; // overflow  <->  l + (r-l)/2
    mergeSort(a, l, mid);
    mergeSort(a, mid+1, r);  
    int *arr = new int[r-l+1];  
    int k = 0;
    int i = l, j = mid + 1;
    while(i <= mid && j <= r) {  
        if(a[i] <= a[j]) {
            arr[k++] = a[i++]; 
        }
        else {
            arr[k++] = a[j++]; // ans += (mid-i+1);  
        }
    }
    while(i <= mid) arr[k++] = a[i++];
    while(j <= r) arr[k++] = a[j++];
    for(int i = l; i <= r; i++) {
        a[i] = arr[i-l];
    }
    delete []arr;
}

1.15 约瑟夫环

import java.util.LinkedList;
public class Solution {
    public int LastRemaining_Solution(int n, int m) {
        if(n < 1 || m < 1)
            return -1;
        LinkedList<Integer> link = new LinkedList<Integer>();
        for(int i = 0; i < n; i++)
            link.add(i);
        int index = -1;   //起步是 -1 不是 0
        while(link.size() > 1){
            index = (index + m) % link.size();  //对 link的长度求余不是对 n
            link.remove(index);
            index --;
        }
        return link.get(0);
    }
}

1.17 排序数组中某数字出现的次数

int bina(int *a, int len, int data) {
    if(a == NULL || len <= 0) return -1;
    int l = 0, r = len - 1;
    while(l <= r) {
        int mid = (l + r) / 2;
        if(a[mid] == data) return mid;
        else if(data < a[mid]) {
            r = mid - 1;
        }
        else l = mid+1;
    }
    return -1;
 }

2. LinkedList

linkedlist_summary

2.1 easy:

在 O(1) 时间删除链表节点， ✔️

删除单链表倒数第 n 个节点， ✔️

求单链表的中间节点， ✔️

判断单链表是否存在环， ✔️

从尾到头打印链表, 递归 ok.， ✔️

链表中倒数第k个结点 ok.， ✔️

判断两个无环单链表是否相交， ✔️

两个链表相交扩展：求两个无环单链表的第一个相交点， ✔️

两个链表的第一个公共结点， ✔️

旋转单链表

题目描述：给定一个单链表，设计一个算法实现链表向右旋转 K 个位置。
举例：给定 1->2->3->4->5->6->NULL, K=3
则4->5->6->1->2->3->NULL

环路的入口点

在第 4 题两个指针相遇后，让其中一个指针回到链表的头部，另一个指针在原地，同时往前每次走一步，当它们再次相遇时，就是在环路的入口点。

2.2 medium:

反转链表 next=head->next, head->next=pre, pre=head, head=next; 4步 ok， ✔️

翻转部分单链表举例：1->2->3->4->5->null, from = 2, to = 4 结果：1->4->3->2->5->null

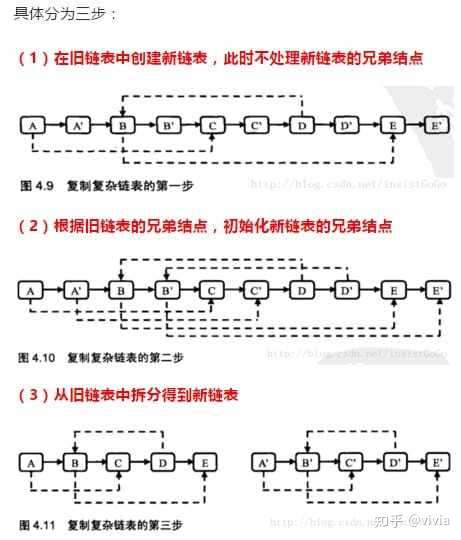
复杂链表的复制 ok， ✔️

链表划分（题目描述：给定一个单链表和数值x，划分链表使得小于x的节点排在大于等于x的节点之前）

单链表排序

合并两个或k个有序链表 ok，递归 (三元运算符).

删除链表重复结点链表1->2->3->3->4->4->5 处理后为 1->2->5. first->next=head, last, p 三针， ✔️

链表中环的入口结点， ✔️

单链表排序 or 合并两个或k个有序链表

struct Node { Node *next; int value; }; 
/* 你一定要相信递归是一个强大的思想 */
Node* mergeList(Node* head1, Node* head2) { // 有序链表的合并
    if(head1 == NULL) return head2;
    if(head2 == NULL) return head1;
    Node* tmp;
    if(head1->value < head2->value) {
        tmp = head1;
        head1 = head1->next;
    }
    else {
        tmp = head2;
        head2 = head2->next;
    }
    tmp->next = mergeList(head1, head2);
    return tmp;
}
Node* mergeSort(Node* head) {
    if(head == NULL) return NULL;
    Node* r_head = head;
    Node* head1 = head;
    Node* head2 = head;
    while(head2->next != NULL && head2->next->next != NULL) {
        head1 = head1->next;
        head2 = head2->next->next;
    }
    if(head1->next == NULL) return r_head; // 只有一个节点
    head2 = head1->next;
    head1 = head;
    r_head = mergeList(mergeSort(head1), mergeSort(head2));
    return r_head;
}

2.3 difficul:

链表求和

—

反转链表:

public ListNode reverseList(ListNode head) {
    ListNode next = null;
    ListNode pre = null

    while (head != null) {
        next = head.next; (保存当前头结点的下个节点)
        head.next = pre;  (将当前头结点的下一个节点指向“上一个节点”，这一步是实现了反转)
        pre = head;       (将当前头结点设置为“上一个节点”)
        head = next;      (将保存的下一个节点设置为头结点)
    }
    return pre;
}

复杂链表的复制:

/*
public class RandomListNode {
    int label;
    RandomListNode next = null;
    RandomListNode random = null;

    RandomListNode(int label) {
        this.label = label;
    }
}
*/

public class Solution {
    public RandomListNode Clone(RandomListNode pHead)
    {
        if(pHead == null)
            return null;
        //复制节点 A->B->C 变成 A->A'->B->B'->C->C'
        RandomListNode head = pHead;
        while(head != null){
            RandomListNode node = new RandomListNode(head.label);
            node.next = head.next;
            head.next = node;
            head = node.next;
        }
        //复制random
        head = pHead;
        while(head != null){
            head.next.random = head.random == null ? null : head.random.next;
            head = head.next.next;
        }
        //折分
        head = pHead;
        RandomListNode chead = head.next;
        while(head != null){
            RandomListNode node = head.next;
            head.next = node.next;
            node.next = node.next == null ? null : node.next.next;
            head = head.next;
        }
        return chead;
    }
}

链表划分：

给定一个单链表和数值x，划分链表使得所有小于x的节点排在大于等于x的节点之前。

你应该保留两部分内链表节点原有的相对顺序。

样例
给定链表 1->4->3->2->5->2->null，并且 x=3
返回** 1->2->2->4->3->5->null**

    public ListNode partition(ListNode head, int x) {
        // write your code here
        if(head == null) return null;
        ListNode leftDummy = new ListNode(0);
        ListNode rightDummy = new ListNode(0);
        ListNode left = leftDummy, right = rightDummy;
        
        while (head != null) {
            if (head.val < x) {
                left.next = head;
                left = head;
            } else {
                right.next = head;
                right = head;
            }
            head = head.next;
        }
        
        right.next = null;
        left.next = rightDummy.next;
        return leftDummy.next;
    }
}

3. String

13 道题搞定 BAT 面试——字符串

字符串

# include <iostream>
# include <vector>
# include <queue>
# include <cstring>

using namespace std;

int main() {
    string x;
    cin >> x;
    sort(x.begin(), x.end());
    reverse(x.begin(), x.end());
    cout << x << endl;
    return 0;
}

3.1 easy:

替换空格， ✔️

反转字符串 abcd -> dcba， ✔️

翻转单词顺序列， I am a student. -> student. a am I， ✔️

旋转字符串， abcde --2位–> cdeab, 若干次旋转操作之后，A 能变成B，那么返回True， ✔️

左旋转字符串 string LeftRotateString(string str, int n),string Reverse(string str)， ✔️

反转字串单词 string ReverseSentence(string str), reverse(str.begin(), str.end()); in lib algorithm

3.2 medium

字符流中第一个不重复的字符 (哈希来存每个字符及其出现的次数，另用一字符串 s 来保存字符流中字符顺序)

第一个只出现一次的字符

字符串全排列 void res(char *str, char *pStr), scanf("%s", str); #include < utility>

字符串转整型 int StrToInt(char* str) ok

字符串的排列 (给定两个字符串 s1 和 s2，第一个字符串的排列之一是第二个字符串的子串)

import java.util.HashMap;
public class Solution {
    HashMap<Character, Integer> map = new HashMap<Character, Integer>();
    StringBuffer s = new StringBuffer();
    //Insert one char from stringstream
    public void Insert(char ch)
    {
        s.append(ch);
        if(map.containsKey(ch)){
            map.put(ch, map.get(ch)+1);
        }else{
            map.put(ch, 1);
        }
    }
  //return the first appearence once char in current stringstream
    public char FirstAppearingOnce()
    {
        for(int i = 0; i < s.length(); i++){
            if(map.get(s.charAt(i)) == 1)
                return s.charAt(i);
        }
        return '#';
    }
}

3.2 difficult

KMP 算法

最长公共前缀

最长回文串 (3.1) 验证回文串 (3.2) 最长回文子串 (3.3) 最长回文子序列

表示数值的字符串

剑指offer: 表示数值的字符

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。例如，字符串”+100″,”5e2″,”-123″,”3.1416″和”-1E-16″都表示数值。但是”12e”,”1a3.14″,”1.2.3″,”±5″和”12e+4.3″都不是。

3.1 easy code

3.1.1 替换空格

for(int i=tail; i>len && i>=0; i--){
    if(str[len] == ' ') {
        str[i--] = '0';
        str[i--] = '2';
        str[i] = '%';
    }
    else {
        str[i] = str[len];
    }
    len--;
}

3.1.4 旋转字符串

class Solution {
    public boolean rotateString(String A, String B) {
        return A.length() == B.length() && (A+A).contains(B);
    }
}

3.1.5 左旋转字符串

字符序列S=”abcXYZdef”,要求输出循环左移3位后的结果，即“XYZdefabc”。是不是很简单？OK，搞定它！

在第 n 个字符后面将切一刀，将字符串分为两部分，再重新并接起来即可。注意字符串长度为 0 的情况。

public class Solution {
    public String LeftRotateString(String str,int n) {
        int len = str.length();
        if(len == 0)
            return "";
        n = n % len;
        String s1 = str.substring(n, len);
        String s2 = str.substring(0, n);
        return s1+s2;
    }
}

3.2 medium code

void res(char *str, char *pStr) {
    if(*pStr == '\0') cout << str << endl;
    for(char *p = pStr; *p != '\0'; ++p) {
        char tmp = *p;
        *p = *pStr;
        *pStr = tmp;
        res(str, pStr+1);
        tmp = *p;
        *p = *pStr;
        *pStr = tmp;
    }
}

字符流中第一个不重复的字符 C++

/class Solution
{
public:
  //Insert one char from stringstream
    
    // vector用来记录字符流
    vector<char> vec;
    // map用来统计字符的个数
    map<char, int> table;
    void Insert(char ch)
    {
        table[ch]++;
        vec.push_back(ch);
    }
  //return the first appearence once char in current stringstream
    char FirstAppearingOnce()
    {
        // 遍历字符流，找到第一个为1的字符
        for (char c : vec) {
            if (table[c] == 1)
                return c;
        }
        
        return '#';
    }

};

字符流中第一个不重复的字符 Java

import java.util.HashMap;
public class Solution {
    HashMap<Character, Integer> map = new HashMap<Character, Integer>();
    StringBuffer s = new StringBuffer();
    //Insert one char from stringstream    
    public void Insert(char ch)    {
        s.append(ch);
        if(map.containsKey(ch)){
            map.put(ch, map.get(ch)+1);
        }else{
            map.put(ch, 1);
        }
    }
  //return the first appearence once char in current stringstream    
    public char FirstAppearingOnce()    {
        for(int i = 0; i < s.length(); i++){
            if(map.get(s.charAt(i)) == 1)
                return s.charAt(i);
        }
        return '#';
    }
}

4. Binary Tree

算法&数据结构， 20Tree

4.1 easy

递归：求二叉树中的节点个数， ✔️

递归：求二叉树的最大层数(最大深度) & (最小深度) 最小深度特殊情况：left || right==0 ， ✔️

递归：求二叉树第K层的节点个数 get_k(root.left, k-1) + get_k(root.right, k-1); good ， ✔️

递归：求二叉树第K层的叶子节点个数 if(k==1 and root.left and root.right is null) return 1; ， ✔️

递归：二叉树先序遍历/前序遍历 (fIno(Node* root) { while(1) {if else}

递归：判断两棵二叉树是否结构相同， ✔️

递归：求二叉树的镜像（反转二叉树），（左右递归交换）✔️

递归：对称二叉树（双函数，承接上题二叉树的镜像， good）， ✔️

递归：求二叉树中两个节点的最低公共祖先节点 good ， ✔️

递归：求二叉搜索树的最近公共祖先 good ， ✔️

递归：根据前序和中序重建二叉树， ✔️

双函数，递归

树的子结构,遍历+判断, bool f5(Node* root1, Node* root2), bool son(Node* p1, Node* p2) ， ✔️

判断二叉树是不是平衡二叉树 bool isBalance(Node* root)， int maxHigh(Node* root) ， ✔️

求二叉树的直径（直径长度是任意两个结点路径长度中的最大值）， ✔️

4.2 medium

分层遍历 (判断二叉树是不是完全二叉树) （遍历到了NULL结点，如后续还有非NULL结点）， ✔️

分层遍历 (自下而上分层遍历) bfs + vector< vector < int > >， ✔️

分层遍历 (按之字形顺序打印二叉树)， ✔️

4.3 difficult:

二叉树中和为某一值的路径 void f4(Node* root, int exSum, int curSum, vecotr< int >& path)， ✔️

二叉树下一结点:3情况 (1.有right.child 2.没有right.child,父left.child 3.没有right.child,父right.child)✔️

序列化二叉树， String serialize(TreeNode root), TreeNode deserialize(String data) Queue queue = new LinkedList<>(); ✔️

二叉搜索树的后序遍历序列 bool f6(int* sec, int len)， ✔️

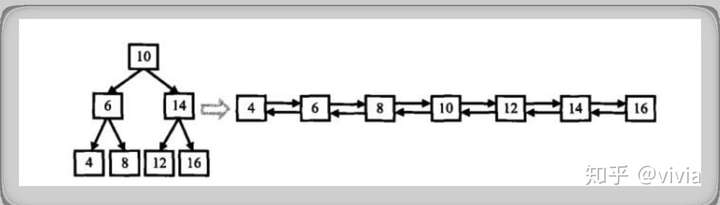
二叉搜索树与双向链表 void convert(Node* root, Node*& pLast) ， ✔️

二叉搜索树的第k个结点， ✔️

二叉查找树节点的删除. 重要

4.1 easy code

4.1.9 二叉树两节点的最低公共祖先

# include <iostream>
# include <vector>
# include <cstring>

using namespace std;

struct Node {
    Node* lchild;
    Node* rchild;
    int value;
    Node(): value(0), lchild(NULL), rchild(NULL) {}
    
};

vector<Node*> vec1;
vector<Node*> vec2;

/**

  1. 找到目标节点1，寻找路径，存放在 vec1 中.
  2. 找到目标节点2，寻找路径，存放在 vec2 中.
  3. 同时遍历 2 个 

*/
bool getNodePath(Node* root, Node* target, vector<Node*>& vec) {
    if (root == NULl) {
        return false;
    }
    vec.push_back(root);
    if (root == target) {
        return true;
    }
    bool flag = false;
    flag = getNodePath(root->lchild, target, vec)
    if (!flag && root->rchild) {
        flag = getNodePath(root->rchild, target, vec)
    }
    if (!flag) {
        vec.pop_back();
    }
    return flag;
}

Node* getCom(const vector<Node*>& v1,  const vector<Node*>& v2) {
    vector<Node*>::const_iterator it1 = v1.begin();
    vector<Node*>::const_iterator it2 = v2.begin();
    
    Node* pLast = NULL;

    while (it1 != v1.end() && it2 != v2.end()) {
        if (*it1 != *it2) {
            break;
        }
        pLast = *it1;
        it1++;
        it2++;
    }
    return pLast;
}
int main() {
    retunr 0;
}

4.1.10 求二叉搜索树的最近公共祖先

Node* lowestCommonAncestor(Node* root, Node* p, Node* q) {
    if (root == NULL || p == NULL || q == NULL) {
        return NULL;
    } 
    if (root->value > p->value && root > q->value) {
        return lowestCommonAncestor(root->lchild, p, q);
    } 
    if (root->value < p->value && root < q->value) {
        return lowestCommonAncestor(root->rchild, p, q);
    } 
    return root;
}

4.1.11 前序中序重建二叉树

Node* f3(int* pre, int* ino, int len) { // pre : 1, 2, 4, 7, 3, 5, 6, 8  ino : 4, 7, 2, 1, 5, 3, 8, 6
    if(pre == NULL || ino == NULL || len <= 0) return NULL;
    int r_v = pre[0];
    Node* root = new Node();
    root->value = r_v;
    int i;
    for(i = 0; ; i++) {
        if(ino[i] == r_v) break;
    }
    root->lchild = f3(pre+1, ino, i);
    root->rchild = f3(pre+i+1, ino+i+1, len-1-i);
    return root;
}

双函数 + 递归

4.1.12 树2是否是树1的子结构

bool son(Node* p1, Node* p2) {
    if (p2 == NULL) {
        return true;
    }
    if (p1 == NULL) {
        return false;
    }
    if (p1->value == p2->value) {
        return son(p1->lchild, p2-lchild);
    }
}

bool son_tree(Node* root1, Node* root2) {
    if (root2 == NULL) {
        return true;
    }
    if (root1 == NULL) {
        return false;
    }
    if (root1->value == root2->child) {
        return son(root1, root2);
    }
    bool flag = false
    flag = son_tree(root1->lchild, root2);
    if (!flag) {
        return son_tree(root1->rchild, root2);
    }
}

4.1.13 平衡二叉树

bool isBalanced(Node* root) {
    if(root == NULL)
        return true;
    return (-1 <= (maxHigh(root->lchild) - maxHigh(root->rchild)) <= 1)
        && isBalanced(root->lchild) && isBalanced(root->lchild);
}

int maxHigh(Node* root){
    if(root == NULL)
        return 0;
    return max(maxHigh(root->lchild), maxHigh(root->rchild))+1;
}

4.1.14 求二叉树的直径

private int diamHelper(TreeNode root){
    if(root == null)
        return 0;
    int left = diamHelper(root.left);
    int right = diamHelper(root.right);
    path = Math.max(path, left + right);
    return Math.max(left, right) + 1;
}

4.2 medium code

4.2.1 判断二叉树是不是完全二叉树

bool checkCompleteTree(Node* root) {

    bool flag = true;
    queue<Node*> q;

    if (root == null)
        return true;

    q.push(root);

     while(!q.empty()){  
         for (int i = 0; i < q.size(); ++i) {  
             Node* tmp = q.front();
             q.pop();
            
             if (tmp->lchild == NULL && tmp->rchild != NULL){
                 flag = false;
                 break;
             }
             if (tmp->left != NULL)
                 que.push(tmp->left);
             if (tmp->right != NULL)
                 que.push(tmp->right);
         }
    }
    return flag;    
}

4.2.2 分层遍历 (自下而上分层遍历)

vector<vector<int>> bfs(Node* root) {

    vector <vector<int> > ans;

    if (root == NULL)
        return ans;

    queue<Node*> q;
    
    q.push(root);

     while(!q.empty()) {  
     
         vector<int> tv;
         
         for (int i = 0; i < q.size(); ++i) {  
             Node* tmp = q.front();
             q.pop();
             if (tmp->lchild == NULL && tmp->rchild != NULL){
                 flag = false;
                 break;
             }
             if (tmp->left != NULL)
                 que.push(tmp->left);
             if (tmp->right != NULL)
                 que.push(tmp->right);
             
             tv.push_back(tmp->value);
         }
         ans.push_back(tv)
    }
    return flag;    
}

// reverse(res[i].begin(), res[i].end());

4.3 difficult code

4.3.1 二叉树中和为某一值的路径

void f4(Node*, int, int, vector<int>&);
void f4(Node* root, int exSum) {
    if(root == NULL) return;
    vector<int> V;
    int curSum = 0;
    f4(root, exSum, curSum, V);
}
void f4(Node* root, int exSum, int curSum, vecotr<int>& path) {
    curSum += root->value;
    path.push_back(root->value);
    if(curSum == exSum && root->lchild == NULL && root->rchild == NULL) {
        //; 打印vector中的路径
    }
    if(root->lchild) f4(root->lchild, exSum, curSum, path);
    if(root->rchild) f4(root->rchild, exSum, curSum, path);
    curSum -= root->value;
    path.pop_back();
}

4.3.3 序列化二叉树

public String serialize(TreeNode root) {
    if(root == null)
        return "#,";
    StringBuffer res = new StringBuffer(root.val + ",");
    res.append(serialize(root.left));
    res.append(serialize(root.right));
    return res.toString();
}

// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
    String [] d = data.split(",");
    Queue<String> queue = new LinkedList<>();
    for(int i = 0; i < d.length; i++){
        queue.offer(d[i]);
    }
    return pre(queue);
}

public TreeNode pre(Queue<String> queue){
    String val = queue.poll();
    if(val.equals("#"))
        return null;
    TreeNode node = new TreeNode(Integer.parseInt(val));
    node.left = pre(queue);
    node.right = pre(queue);
    return node;
}

4.3.4 二叉搜索树后序遍历的结果

bool f6(int* sec, int len) {
    if(sec == NULL) return false;
    if(len <= 1) return true;
    int i, rv = sec[len-1];
    for(i = 0; i < len-1; i++) {
        if(sec[i] > rv) break;
    }
    for(int j = i; j < len-1; j++) {
        if(sec[j] < rv) return false;
    }
    return f6(sec, i) && f6(sec+i, len-i-1);
}

4.3.5 二叉搜索树与双向链表

void convert(Node* root, Node*& pLast) {
    if(root == NULL) return;
    if(root->lchild) convert(root->lchild, pLast);
    
    Node* pCur = root;
    pCur->lchild = pLast;
    
    if(pLast) pLast->rchild = pCur;
    pLast = pCur;
    
    if(root->rchild) convert(root->rchild, pLast);
}

4.3.6 二叉搜索树的第k个结点

给定一棵二叉搜索树，请找出其中的第k小的结点。例如，（5，3，7，2，4，6，8）中，按结点数值大小顺序第三小结点的值为4。

因为二叉搜索树按照中序遍历的顺序打印出来就是排好序的，所以，我们按照中序遍历找到第k个结点就是题目所求的结点。

class Solution {
    public int kthSmallest(TreeNode root, int k) {
        if(root == null)
             return Integer.MIN_VALUE;
        Stack<TreeNode> stack = new Stack<>();
        int count = 0;
        TreeNode p = root;
        while(p != null || !stack.isEmpty()){
            if(p != null){
                stack.push(p);
                p = p.left;
            }else{
                TreeNode node = stack.pop();
                count ++;
                if(count == k)
                    return node.val;
                p = node.right;
            }
        }
        return Integer.MIN_VALUE;
    }
}

5. 递归 / 回溯

5.1 斐波拉契

斐波拉契数列 & 跳台阶 & 变态跳台阶 2 * Fib(n-1). ， ✔️

矩形覆盖， ✔️

5.2 回溯

矩阵中的路径(BFS)

机器人的运动范围(DFS)

public int count(int threshold, int rows, int cols, int i, int j, int[][] flag){
    if(i<0 || j<0 || i>=rows || j>=cols || sum(i)+sum(j) > threshold || flag[i][j] == 1){
        return 0;
    }
    flag[i][j] = 1;
    return 1 + count(threshold, rows, cols, i - 1, j, flag) + 
        count(threshold, rows, cols, i + 1, j, flag) +
        count(threshold, rows, cols, i, j - 1, flag) +
        count(threshold, rows, cols, i, j + 1, flag);
}

5.3 位运算

二进制中1的个数 n & n-1.， ✔️

数值的整数次方 dp. ， ✔️

数组中只出现一次的数字 ok. ， ✔️

6. Stack & Queue & heap

Stack & Queue

用两个栈实现队列 ， ✔️

包含min函数的栈 ， ✔️

栈的压入、弹出序列

6.1 用两个栈实现队列

class MyQueue {
    Stack<Integer> input = new Stack<Integer>();
    Stack<Integer> output = new Stack<Integer>();
    /** Push element x to the back of queue. */
    public void push(int x) {
        input.push(x);
    }
    /** Removes the element from in front of queue and returns that element. */
    public int pop() {
        peek();
        return output.pop();
    }
    /** Get the front element. */
    public int peek() {
        if(output.isEmpty()){
            while(!input.isEmpty())
                output.push(input.pop());
        }
        return output.peek();
    }
    /** Returns whether the queue is empty. */
    public boolean empty() {
        return input.isEmpty() && output.isEmpty();
    }
}

6.2 包含min函数的栈

class MinStack {
    Stack<Integer> stack = new Stack<Integer>();
    Stack<Integer> temp = new Stack<Integer>();
    
    public void push(int x) {
        stack.push(x);
        if(temp.isEmpty() || temp.peek() >= x)
            temp.push(x);
    }
    
    public void pop() {
        int x = stack.pop();
        int min = temp.peek();
        if(x == min)
            temp.pop();
    }
    
    public int top() {
        return stack.peek();
    }
    
    public int getMin() {
        return temp.peek();
    }
}

6.3 栈的 push pop 序列

栈的 push pop 序列
1 2 3 4 5
4 3 5 1 2

import java.util.ArrayList;
import java.util.Stack;
public class Solution {
    public boolean IsPopOrder(int [] pushA, int [] popA) {
        if(pushA.length != popA.length || 
               pushA.length == 0 ||
               popA.length == 0)
            return false;
        Stack<Integer> stack = new Stack<>();
        int index = 0;
        for(int i = 0; i < pushA.length; i++){
            stack.push(pushA[i]);
            while(!stack.empty() && stack.peek() == popA[index]){
                stack.pop();
                index++;
            }
        }
        return stack.empty();
    }
}

7. PriorityQueue

最小的K个数

数据流中的第K大元素

滑动窗口最大值

前K个高频单词

优先队列

8. Dynamic Programming

爬楼梯， ✔️

不同路径 II ， ✔️

编辑距离， ✔️

不同路径 II

如果当前没有障碍物，dp[m][n] = dp[m - 1][n] + dp[m][n - 1]
如果有障碍物，则dp[m][n] = 0

编辑距离

如果单词1第i+1个字符和单词2第j+1个字符相同，那么就不用操作，则DP[i + 1][j + 1] = DP[i][j];

如果不相同,则有三种可能操作，即增，删，替换。则取这三种操作的最优值，即dp[i + 1][j + 1] = 1 + Math.min(dp[i][j], Math.min(dp[i][j + 1], dp[i + 1][j]));

8.1 一维DP

连续子数组的最大和 // dp: F[i] = max(a[i], F[i-1]+a[i]);

8.2 二维DP

布尔数组

Longest Palindromic Substring/最长回文子串给出一个字符串S，找到一个最长的连续回文串。

Interleaving String/交错字符串输入三个字符串s1、s2和s3，判断第三个字符串s3是否由前两个字符串s1和s2交替而成且不改变s1和s2中各个字符原有的相对顺序。

数字数组

Unique Paths II/不同路径 (初始化很重要) ，起点到终点有多少条不同路径，向右或向下走。

Minimum Path Sum 矩阵左上角出发到右下角，只能向右或向下走，找出哪一条路径上的数字之和最小。
Edit Distance/编辑距离求两个字符串之间的最短编辑距离，即原来的字符串至少要经过多少次操作才能够变成目标字符串，操作包括删除一个字符、插入一个字符、更新一个字符。
Distinct Subsequences/不同子序列给定S和T两个字符串，问把通过删除S中的某些字符，把S变为T有几种方法？

补充：京东2019实习编程题-删除0或部分字符使其成为回文串见笔试整理总结

8.3 三维DP

9. 剑指offer

算法学习5

diffcult

整数中1出现的次数 (判断每一位，比如百位分别为 1, 0, 2~9, 后2种情况可合并)
LRU Cache 需要深入学习Java的Map的内部实现

vector: vector::iterator, Modifiers (push_back, pop_back, insert)

array : len = sizeof(arr)/sizeof(int)

import java.util.ArrayList;
import java.util.LinkedList;
public class Solution {
    public ArrayList<Integer> maxInWindows(int [] num, int size){
        ArrayList<Integer> res = new ArrayList<Integer>();
        LinkedList<Integer> deque = new LinkedList<Integer>();
        if(num.length == 0 || size == 0)
            return res;
        for(int i = 0; i < num.length; i++){
            if(!deque.isEmpty() && deque.peekFirst() <= i - size)
                deque.poll();
            while(!deque.isEmpty() && num[deque.peekLast()] < num[i])
                deque.removeLast();
            deque.offerLast(i);
            if(i + 1 >= size)
                res.add(num[deque.peekFirst()]);
        }
        return res;
    }
}

10. shopee & sina

shopee

下一个更大元素 (Stack < Integer > (), Map < Int, Int > map, map.getOrDefault(nums1[i], -1); 序列为 9 2 1 4 借助栈实现，判断栈顶和下一个元素的大小， ✔️

鸡蛋掉落 (DP问题，难)

google 扔鸡蛋，原题是 100 层楼，鸡蛋无限，答案 14 次。， ✔️

二叉树的右视图 (层次遍历) res.push_back(q.back()->val);， ✔️

复杂链表指针， ✔️

K 个一组翻转链表 1->2->3->4->5，当 k = 2 时，应返: 2->1->4->3->5 ， ✔️

不同的二叉搜索树， ✔️

零钱兑换完全背包问题，i=coins[j];i<=amount;，dp[i]=Math.min(dp[i],dp[i-coins[j]]+1); ✔️

相交链表

有效的括号（Stack来解决）， ✔️

两数相加

[LeetCode] 887. Super Egg Drop 超级鸡蛋掉落， ✔️

1	dp[i][j] = min(dp[i][j], max(dp[i - 1][k - 1], dp[i][j - k]) + 1) ( 1 <= k <= j )

之后可以再优化.

class Solution:
    def isValid(self, s):
        """
        :type s: str
        :rtype: bool
        """
        stack = list()
        match = {'{':'}', '[':']', '(':')'}
        for i in s:
            if i == '{' or i == '(' or i == '[':
                stack.append(i)
            else:
                if len(stack) == 0:
                    return False

                top = stack.pop()
                
                if match[top] != i:
                    return False

        if len(stack) != 0:
            return False
        return True

sina

两数之和 (链表 carry) ， ✔️

最大子序和， ✔️ 分治？

搜寻名人 (if (knows(res, i)) res = i;) ， ✔️

连续出现的数字， ✔️

搜索二维矩阵， ✔️

排序链表

翻转二叉树， ✔️

买卖股票的最佳时机系列

字符串转整型

无重复字符的最长子串， ✔️ （借助hashmap）

Tencent

Minimum Factorization 最小因数分解
[LeetCode 最小基因变化（广度优先搜索）]

class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        int carry = 0;
        ListNode* fakeHead = new ListNode(-1);
        ListNode* curr = fakeHead;
        while (l1 != NULL || l2 != NULL | carry != 0) {
            if (l1 != NULL) {
                carry += l1->val;
                l1 = l1->next;
            }
            if (l2 != NULL) {
                carry += l2->val;
                l2 = l2->next;
            }
            ListNode* node = new ListNode(carry % 10);
            carry /= 10;
            curr->next = node;
            curr = node;
        }
        return fakeHead->next;
    }
};

11. 海量数据

m_15 二叉树非递归的先根遍历和中序遍历 (必会数据结构之一)

void fPre(Node* root) { // 先根遍历  根->左->右
    Node* p = root;
    stack<Node*>  S;
    while(1) {
        if(p != NULL) {
            cout << p->value << ' ';
            S.push(p);
            p = p->lchild;
        }
        else {
            if(S.empty()) return;
            p = S.top(); S.pop();
            p = p->rchild;
        }
    }
}
void fIno(Node* root) {
    Node* p = root;
    stack<Node*> S;
    while(1) {
        if(p != NULL) {
            S.push(p);
            p = p->lchild;
        }
        else {
            if(S.empty()) return;
            p = S.top(); S.pop();
            cout << p->value <<  ' ';
            p = p->rchild;
        }
    }
}